Tuenti Challenge 8

In this post I'll explain the reasoning behind my solutions to the problems of the Tuenti Challenge 8.

List of challenges (you can check the problem statements here):

Waffle love

Security by doorscurity

Challenge 1 - Waffle love

There is not much to explain for this one. If $n$ and $m$ are the numbers of vertical and horizontal lines of the waffle, the number of holes will be $(n - 1) (m - 1)$.

def waffleHoles(n, m):
  return (n - 1) * (m - 1)

Challenge 2 - Hidden numbers

In this problem we deal with the representation of base-$n$ numbers, where $2$ $\le$ $n$ $\le$ $26$. The problem asks to compute the maximum and minimum number that we can represent in this base (starting with a non-zero value) and return $max - min$ as a result.

We'll receive a string as an input, with all the chars different in it. As a first step we'll compute the base just by looking at the length of the string.

For the $max$ number, how do you construct the biggest number in base-10 with the numbers $[0..9]$? $9876543210$, right?. Then, for a base-$n$ number it will be given by the expression: $$max = \sum_{i=1}^{n - 1} i n^i$$

The $min$ case is a little bit tricky. If we assume that there is no leading zero, again, for the base-10 case it would be $1023456789$. We just exchanged the $0$ and the $1$ and voilá!. For our base-$n$ case: $$min = n^{n - 1} + \sum_{i=0}^{n - 3} (n - i - 1) n^i$$

And now some code implementing the idea:

def hidden(word):
  base = len(word)
  max_value = sum([i * base ** i for i in range(1, base)])
  min_value = base ** (base - 1) + sum([(base - i - 1) * base ** i for i in range(base - 2)])

  return max_value - min_value

Challenge 3 - Scales

So, music time!

Summarizing the problem: We are going to receive a set of musical notes and we have to return all the major and natural minor scales that can match these notes.

To simplify the problem we are going to keep only the following notes: $A, A\#, B, C, C\#, D, D\#, E, F, F\#, G, G\#$. Why would we need $Cb$ if it's equivalent to $F\#$?

Now, let's generate the 24 scales! The first step for this is to know the half-step between notes and the progression of both scales:

W = whole_step = True
H = half_step = not whole_step

major_scale = [W, W, H, W, W, W, H]
natural_minor_scale = [W, H, W, W, H, W, W]

step = {
    'A': 'A#',
    'A#': 'B',
    'B': 'C',
    'C': 'C#',
    'C#': 'D',
    'D': 'D#',
    'D#': 'E',
    'E': 'F',
    'F': 'F#',
    'F#': 'G',
    'G': 'G#',
    'G#': 'A'
}

Once we have this, generating the scales is piece of cake:

def generate_scale_set(note, scale):
    scale_set = set()

    for step_type in scale:
        if step_type == half_step:
            note = step[note]
        else:
            note = step[step[note]]
        scale_set.add((note,))

    return scale_set

all_notes = ['A', 'A#', 'B', 'C', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#']
major_scales = {x: generate_scale_set(x, major_scale) for x in all_notes}
natural_minor_scales = {x: generate_scale_set(x, natural_minor_scale) for x in all_notes}

Now that we have the scales we are all setup to solve our problem. Supposing that $notes$ is a set with the notes of the input (converted to our equivalent set of notes), the solution would be:

def scales(notes):
  possible_scales = []

  # major scales
  for note in all_notes:
    if notes.issubset(major_scales[note]):
      possible_scales.append('M' + note)

  # minor natural scales
  for note in all_notes:
    if notes.issubset(natural_minor_scales[note]):
      possible_scales.append('m' + note)

  return 'None' if len(possible_scales) == 0 else ' '.join(possible_scales)

Challenge 4 - Brave Knight

Ingredients: 2D Grid, one source, two sequential destinations, obstacles, lava, trampolines and horse chess-style jumps!

Well, we can reduce this problem to a double shortest-path problem, one between the knight and the princess, and other between the princess and the destination.

In this case, every jump has the same cost, so a breadth-first search will be fine. Starting with the Knight, we generate the possible jumps. If $(row, col)$ is the position of the knight, we have 8 possible jumps, which are the following:

$(row + 2, col + 1)$,$(row + 2, col - 1)$,$(row - 2, col + 1)$,$(row - 2, col - 1)$,$(row + 1, col + 2)$,$(row + 1, col - 2)$,$(row - 1, col + 2)$,$(row - 1, col - 2)$.

In the case of trampolines the jumps will be of length $\pm 4$ and $\pm 2$. Now, given a position we can generate all the possible new jumps:

def open_nodes(position, double_jumps, lava_positions, rows, cols):
    def is_valid(p):
        return not p in lava_positions and 0 <= p[0] < rows and 0 <= p[1] < cols

    possibles = set()
    big = 2, small = 1

    if position in double_jumps:
        big *= 2
        small *= 2

    possibles.add((position[0] + big, position[1] + small))
    possibles.add((position[0] + big, position[1] - small))
    possibles.add((position[0] - big, position[1] + small))
    possibles.add((position[0] - big, position[1] - small))

    possibles.add((position[0] + small, position[1] + big))
    possibles.add((position[0] + small, position[1] - big))
    possibles.add((position[0] - small, position[1] + big))
    possibles.add((position[0] - small, position[1] - big))

    return filter(is_valid, possibles)

Now we'll use this function to implement our breadth-first search algorithm:

def bfs(source, destination, double_jumps, lava_positions, rows, cols):
    visited = set()
    actual = source
    solution = None

    # possible destinations from source position
    to_visit = map(lambda x: (x, 1), open_nodes(actual, double_jumps, lava_positions, rows, cols))

    while solution is None and len(to_visit) > 0:
        # we get the first position and its cost from the queue
        position = to_visit[0][0]
        position_cost = to_visit[0][1]

        # remove the head of the queue
        to_visit = to_visit[1:]

        # mark the position as visited
        visited.add(position)

        # reached the destination, return the number of jumps
        if position == destination:
            return position_cost

        # get and add to the queue new positions reachable from the actual position
        new_to_visit = open_nodes(position, double_jumps, lava_positions, rows, cols)
        for n in new_to_visit:
            if n not in visited and n not in map(lambda x: x[0], to_visit):
                to_visit.append((n, position_cost + 1))

    # impossible to reach from source to destination
    return None

And finally, we use our BFS algorithm to solve our problem!

def brave_knight(source, princess, destination, double_jumps, lava_positions, rows, cols):
  source_to_princess = bfs(source, princess, double_jumps, invalids, rows, cols)
  princess_to_destination = None

  if source_to_princess is not None:
      princess_to_destination = bfs(princess, destination, double_jumps, invalids, rows, cols)

  if princess_to_destination is None:
      return 'IMPOSSIBLE'
  else:
      return str(source_to_princess + princess_to_destination)

Challenge 5 - DNA Splicer

It's bioinformatics time!

We have a bunch of strings and we have to get two identical sequences by aligning some of them, so... OK, we can start with two strings that have the same prefix and then try to concatenate with some of the rest strings.

Fingers crossed... nope. Sometimes we were wrong at the beginning, or in the middle of the process. Let's read the notes again... "There are at most 18 parts". Somebody said backtracking? Let's go for it:

def backtracking(sequence_1, sequence_2, indexes, sequences):
    # we keep the shortest sequence in sequence_1
    if len(sequence_1) > len(sequence_2):
        temp = sequence_1
        sequence_1 = sequence_2
        sequence_2 = temp

    for index, seq in enumerate(sequences):
        # only not used sequences
        if index in indexes:
            continue

        # we form a new sequence concatenating
        new_sequence_1 = sequence_1 + seq

        # sequence match, we found it!
        if new_sequence_1 == sequence_2:
            indexes.append(index)
            indexes.sort()
            return ','.join(map(lambda x: str(x + 1), indexes))

        # we didn't have a match, but still the bigger sequence starts with the smaller, continue the backtracking
        elif new_sequence_1.startswith(sequence_2) or sequence_2.startswith(new_sequence_1):
            new_indexes = list(indexes)
            new_indexes.append(index)

            call = aux(new_sequence_1, sequence_2, new_indexes)
            if call is not None:
                return call
    return None

Eeeh... but what are the initial arguments of our backtracking function? We'll have to try with all the pairs of strings that have a common prefix:

def dna(sequences):
    solution = None

    for i, seq_1 in enumerate(sequences):
        if solution is not None:
            break
        for j, seq_2 in enumerate(sequences):
            if i >= j:
                continue
            if seq_1.startswith(seq_2) or seq_2.startswith(seq_1):
                solution = backtracking(seq_1, seq_2, [i, j], sequences)
                if solution is not None:
                    return solution

Well, ready to go. We only need to connect to the server, retrieve the sequences and solve the cases until we get the key!

from telnetlib import Telnet

tn = Telnet(host='52.49.91.111', port=3241)

tn.read_until('\n')
tn.read_until('\n')
tn.write('SUBMIT\n')

while True:
    response = tn.read_until('\n')
    if 'key' in response:
        print(response)
        break

    sequences = tn.read_until('\n').split()
    tn.write(dna(sequences) + '\n')

Challenge 6 - Button Hero

Did you say ~~job~~ note scheduling? This is a typical dynamic programming problem. First, let's create a class to compute the start and the end time from the input data:

class Note:
    def __init__(self, start, length, speed, score):
        self.start = start / speed
        self.end = self.start + length / speed
        self.score = score

The idea is to sort the notes by end time in ascending order and create a table (array) of $n$ elements, where $n$ is the number of notes. Now, we compute the values for each entry of the table in the following way: For each $i \in [0..n-1]$ we compute:

\begin{equation*}table[i] = \left \{ \begin{array}{lc} note_0.score & i = 0\\ \max \left\{ \begin{array}{l} \text{Maximum by including } note_i\\ table[i - 1]\\ \end{array} \right . & 1 \leq i \le n \end{array} \right . \end{equation*}

Note that $table[i-1]$ is equivalent to "Maximum by excluding $note_i$". Now, for computing the maximum value including the $i^{th}$ note we will have to go back in the table and find the latest note compatible with $note_i$. Summarizing, we want to find a $j$ such that:

$$ j \mid note_j.end < note_i.start \wedge \not\exists k : k > j \mid note_k.end < note_i.start $$

If there is not such $j$, the maximum value will be just $note_i.score$. On the other hand, if it exists the maximum value will be $note_i.score + table[j]$.

Now it's code time! Let's implement this idea:

def schedule(notes):
    notes = sorted(notes, key=lambda n: n.end)

    n = len(notes)
    table = [0 for _ in range(n)]

    table[0] = notes[0].score

    for i in range(1, n):
        score = notes[i].score
        l = binary_search(notes, i)
        if l != -1:
            score += table[l]

        table[i] = max(score, table[i - 1])

    return table[n - 1]

In this case we use binary search in order to search the latest compatible note, instead of going one by one through the previous notes. This reduces the time complexity of the search ($\mathcal{O}(log\ n)$ vs $\mathcal{O}(n)$).

Also notice that when parsing the notes we can find notes that have the same start and end, so we first combine these notes into a new one with the sum of both scores.

To finish here you have also the implementation of the binary search, just in case ;).

def binary_search(notes, start_index):
    lo = 0
    hi = start_index - 1

    while lo <= hi:
        mid = (lo + hi) // 2
        if notes[mid].end < notes[start_index].start:
            if notes[mid + 1].end < notes[start_index].start:
                lo = mid + 1
            else:
                return mid
        else:
            hi = mid - 1
    return -1

Challenge 7 - Unknown cartridge

When we click on the game boy cartridge image we'll download an unknown file of 32K. First thing that I tried was...

❯ file unknown
unknown: Game Boy ROM image: "UNKNOWN" (Rev.01) [ROM ONLY], ROM: 256Kbit

Surprise! A game boy ROM. You could load the ROM with a game boy emulator and see a lot of letters appearing in the screen, but we are not going to copy them by hand, isn't it?

❯ strings unknown | head -n 2
3>UNKNOWN
cGlrYWNodSBrYSBrYSBrYSBrYSBrYSBwaXBpIHBpa2FjaHUga2Ega2Ega2Ega2Ega2Ega2EgcGlwaSBwaWthY2h1IHBpa2FjaHUga2Ega2Ega2Ega2EgcGljaHUgcGlrYWNodSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaWNodSBwaWthY2h1IGthIGthIGthIGthIGthIHBpcGkgcGlrYWNodSBrYSBrYSBrYSBrYSBrYSBrYSBrYSBwaWthY2h1IHBpIHBpIHBpcGkgcGlrYWNodSBwaWNodSBwaWthY2h1IHBpIHBpcGkgcGlrYWNodSBwaSBwaSBwaSBwaWNodSBwaWthY2h1IGthIGthIGthIGthIGthIHBpcGkgcGlrYWNodSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaWNodSBwaWthY2h1IHBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpcGkgcGlwaSBwaXBpIGNodSBrYSBwaWNodSBwaWNodSBwaWNodSBwaWNodSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaSBwaXBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpIHBpcGkgcGkgcGkgcGkgcGlwaSBwaSBwaXBpIHBpa2EgcGkgcGkgcGkgcGkgcGkgcGkgcGkgcGkgcGkgcGk=

The second line seems like base64...

❯ strings unknown | head -n 2 | tail -n 1 | base64 --decode
pikachu ka ka ka ka ka pipi pikachu ka ka ka ka ka ka pipi pikachu pikachu ka ka ka ka pichu pikachu pi pi pi pi pi pi pi pi pi pi pi pichu pikachu ka ka ka ka ka pipi pikachu ka ka ka ka ka ka ka pikachu pi pi pipi pikachu pichu pikachu pi pipi pikachu pi pi pi pichu pikachu ka ka ka ka ka pipi pikachu pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pichu pikachu pi pi pi pi pi pi pi pi pi pi pipi pipi pipi chu ka pichu pichu pichu pichu pi pi pi pi pi pi pi pi pi pi pipi pi pi pi pi pi pi pi pipi pi pi pi pipi pi pipi pika pi pi pi pi pi pi pi pi pi pi

So yep, now we have a Pikachu singing... After searching a little I found this. Really? A 1-1 mapping to the brainfuck programming language.

First I tried to run the program with an interpreter, but if you search a little about brainfuck and see the translation of the pikalang program you'll see that it contains a ']' before '[' which doesn't make sense.

Or does it? Do you remember the image of the cartridge? It was backwards... so let's try this.

❯ strings unknown | head -n 2 | tail -n 1 | base64 --decode | awk '{ for (i=NF; i>1; i--) printf("%s ", $i); print $1; }'
pi pi pi pi pi pi pi pi pi pi pika pipi pi pipi pi pi pi pipi pi pi pi pi pi pi pi pipi pi pi pi pi pi pi pi pi pi pi pichu pichu pichu pichu ka chu pipi pipi pipi pi pi pi pi pi pi pi pi pi pi pikachu pichu pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pi pikachu pipi ka ka ka ka ka pikachu pichu pi pi pi pikachu pipi pi pikachu pichu pikachu pipi pi pi pikachu ka ka ka ka ka ka ka pikachu pipi ka ka ka ka ka pikachu pichu pi pi pi pi pi pi pi pi pi pi pi pikachu pichu ka ka ka ka pikachu pikachu pipi ka ka ka ka ka ka pikachu pipi ka ka ka ka ka pikachu

And now let's try to execute this pikalang program... Bingo! P1K4L4NG_R00LZ.

Challenge 8 - Security by doorscurity

If you do a couple of examples by hand, you'll notice that you have to find the instant of time where the first door have 0 seconds left to open, the second one 1 second left to open...

Let's take the first example: first door opens every 7 seconds and 5 remaining for the next opening, and the second door opens every 9 seconds and 6 remaining for the next opening.

If you apply the previous reasoning, you want to find an instant with restrictions: 7 seconds of cycle with 5 remaining and 9 seconds of cycle with (6-1)=5 remaining.

In this case the remaining are the same for both doors, so we have only to wait 5 seconds! Let's take the second example:

5 seconds of cycle with 3 remaining, 9 seconds of cycle with (6-1)=5 remaining, and 7 seconds of cycle with (5-2)=3 remaining. Now let me rewrite this in other way:

\begin{align*} x & \equiv 3 \mod 5 \\ x & \equiv 5 \mod 9 \\ x & \equiv 3 \mod 7 \\ \end{align*}

This is a congruence system, $x$ represents our instant of time, the remainders indicate the remaining seconds of the doors, and the modulus represent the door cycles. If we solve this congruence system we get $x = 248$, the solution to the second example.

If $p$ and $t$ are the cycle and the time that has passed from the last opening of the $i^{th}$ door, we will add to our system one of the following congruences (both are equivalent):

\begin{align*} x & \equiv - (t + i) & \mod p \\ x & \equiv p - t - i & \mod p \\ \end{align*}

For solving the congruence system we can use the Chinese remainder theorem, but... if you read about it in wikipedia you'll find "under the condition that the divisors are pairwise coprime". And guess what? Some of the inputs of the problem don't meet this condition.

But no worries, thanks to the power of Internet I could find an implementation of the Chinese remainder theorem that also works for non-pairwise coprime cases :).

In the implementation below, $a$ represents the list of remainders, and $n$ the list of the modulus.

from fractions import gcd

def ext_gcd(a, b):
    v1 = [1, 0, a]
    v2 = [0, 1, b]

    if a > b:
        a, b = b, a
    while v1[2] > 0:
        q = v2[2] / v1[2]
        for i in range(0, len(v1)):
            v2[i] = v2[i] - q * v1[i]
        v1, v2 = v2, v1
    return v2[0], v2[1]

def chinese_remainder(a, m):
    n = len(a)

    a1 = a[0]
    m1 = m[0]

    for i in range(1, n):
        a2 = a[i]
        m2 = m[i]

        g = gcd(m1, m2)

        if a1 % g != a2 % g:
            return None

        p, q = ext_gcd(m1 / g, m2 / g)

        mod = m1 / g * m2
        x = (a1 * (m2 / g) % mod * q % mod + a2 * (m1 / g) % mod * p % mod) % mod

        a1 = x
        if a1 < 0:
            a1 += mod
        m1 = mod

    return a1

Challenge 9 - Scrambled Photo

Rocket science! Seeing the paper shredder and the image you can imagine that the columns of the picture has been shuffled.

After that I found a good implementation of an image unshredder here by Project Nayuki that works pretty good. I used it, scanned the QR codes on both images, and went for the next challenge!

Challenge 10 - Dance

When I first read about returning the number of different ways modulo $10^9 + 7$, I realized that brute force was not an option for this problem.

Then I thought that maybe this is an opportunity to use a divide and conquer strategy, let me explain:

We pick a person from the group of people, let's say that we have the case 4 from the problem statement, with 8 people. If we pick the upper left person, we have 7 possibilities of joining the person with another one (we'll forget about relationships for now).

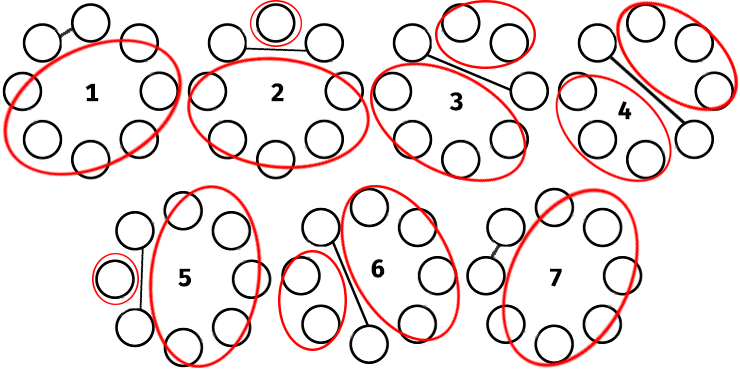
At both sides of the new couple (marked in red) we'll have new groups of people, that can be transformed into new sub-instances of the problem. Both sub-instances can be combined using the rule of product to compute the total number of ways of arranging all the people.

Notice that this transformation also have to reassign indexes to the members of the new sub-groups. This will help us in further optimizations.

The solution for the problem of $n$ people would be, picking a person $p_i$:

$$\sum_{\substack{j\\j \ne i}}^{0 \leq j \le n} sub(i, j)\ sub(j, i)$$

Where $sub(i,j)$ denotes the sub-instance of the problem generated with the people from the $i^{th}$ person to the $j^{th}$ person (both excluded).

The problem has also some base cases:

if $n = 0$, then the ways of arranging people is $1$, if $n$ is odd, it's $0$, and in the case of $n = 2$ we'll return $1$ in the case of compatibility between both persons and $0$ in the case of non-compatibility between them.

$$ \left \{ \begin{array}{l} n = 0: 1\\ n\ mod\ 2\ = 1: 0\\ n = 2 \left \{ \begin{array}{l} 1\ \text{if both persons are compatible}\\ 0\ \text{otherwise} \end{array} \right . \end{array} \right . $$

Now optimizations! When we're pairing the person with all the rest of people we have to check if both persons are compatible. If this is not the case, we can skip the whole call of both sub-groups, because it would be invalid.

Another technique that I used to reduce the computation time is memoization. Look at splits 1-7, 2-5, 3-6. When transformed into sub-instances they will be equivalent (assuming we also have the same compatibilities among them).

So, every time we solve an instance, we store the input and their corresponding relationships with the solution, then when we match another sub-instance that is equivalent, we can return the result without computing it again.

Here you have the implementation (I assure you it can be further optimized).

MEMO = {}

def transform(dancers, src, dst):
    if src > dst:
        temp = src
        src = dst
        dst = temp

    right_idx = []
    for i in dancers:
        if src < i < dst:
            right_idx.append(i)

    left_idx = []
    for i in dancers:
        if i != src and i != dst and i not in right_idx:
            left_idx.append(i)

    return left_idx, right_idx


def divide_and_conquer(dancers, grudges):
    size = len(dancers)
    if size == 0:
        return 1
    elif size < 2:
        return 0
    elif size == 2:
        if not dancers[1] in grudges[dancers[0]]:
            return 1
        else:
            return 0

    h = tuple(dancers)
    if h in MEMO:
        return MEMO[h]

    dancer = dancers[0]

    total = 0
    for i in dancers:
        if i == dancer:
            continue
        if i not in grudges[dancer]:
            left_dancers, right_dancers = transform(dancers, dancer, i)

            if len(left_dancers) <= len(right_dancers):
                first = left_dancers
                second = right_dancers
            else:
                first = right_dancers
                second = left_dancers

            first_sol = divide_and_conquer(first, grudges)

            if first_sol != 0:
                second_sol = divide_and_conquer(second, grudges)
                total += first_sol * second_sol

    MEMO[h] = total
    return total

Challenge 11 - Lasers

The only thing I was sure at the beginning is that we could put lasers in all the rows and columns that are totally empty, good! After that, I found the order in which we should process the items to decide which laser to put in order to achieve the optimal solution.

Even with this order, when with one item I had the choice of putting a horizontal or a vertical laser, I couldn't find the heuristic to choose in an optimal way, so I tried using backtracking. For the test case it was fine, but for the submit cases it was way too slow.

So, in the end I opted to use integer linear programming (ILP) for solving the problem. The formalization for this problem is the following:

Let:

$ n = \text{number of columns of the grid}\\ m = \text{number of rows of the grid} $

$ X = \{x_0, x_1, x_2, ..., x_{n-1}\}\\ Y = \{y_0, y_1, y_2, ..., y_{m-1}\} $

The expression to maximize is:

$$sum(X) + sum(Y)$$

Subject to:

$$ \forall (i, j) \in items : x_i + y_j \leq 1 $$ $$ x_i \in \{0, 1\}\ \forall\ 0 \leq i < n\\ y_i \in \{0, 1\}\ \forall\ 0 \leq i < m $$

Now we can use cvxpy for implementing our problem in an easy way:

from cvxpy import *

def lasers(cols, rows, items):
    X = Bool(cols)
    Y = Bool(rows)
    constraints = []

    for (row, col) in items:
        constraints.append(Y[row] + X[col] <= 1)

    objective = Maximize(sum_entries(X) + sum_entries(Y))
    prob = Problem(objective, constraints)

    return int(round(prob.solve()))

Notice that we can optimize the execution time removing variables that are not necessary (empty rows or columns).

Challenge 12 - Victoria's Secret

First of all, IP and port: nothing on telnet, "This is not the protocol you are looking for" with curl, let's try wget:

❯ wget 52.49.91.111:3240
--2018-05-04 16:05:25--  http://52.49.91.111:3240/
Connecting to 52.49.91.111:3240... connected.
HTTP request sent, awaiting response... 418 I'm a keyboard!
2018-05-04 16:05:25 ERROR 418: I'm a keyboard!.

I'm a keyboard!.

That answer plus the debian hint and the usb to ethernet connector in the image = usbip. I setup a vm with the latest debian and installed the usbip package.

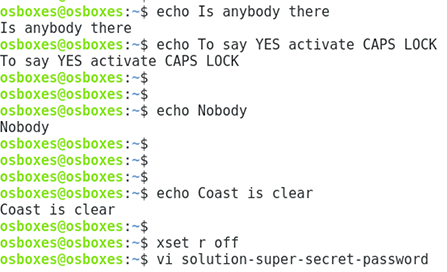
After that, I binded the usb keyboard and the magic started. Something was writing on my terminal, but it introduced a stty command that hid some of the keystrokes.

I'm not going to tell you what happens if you don't follow the instructions, be my guest and try. If after binding the keyboard you switch to a text editor you'll see the hidden message, follow the instructions and all will be fine.

If you are a morse code master, you'll end seeing something like this, and if you're a vi master, you'll get the solution :).

I hope you enjoyed these solutions, and see you next year!

Share on

Twitter Facebook Google+ LinkedIn

Tuenti Challenge 8

Jose Toro

Challenge 1 - Waffle love

Challenge 2 - Hidden numbers

Challenge 3 - Scales

Challenge 4 - Brave Knight

Challenge 5 - DNA Splicer

Challenge 6 - Button Hero

Challenge 7 - Unknown cartridge

Challenge 8 - Security by doorscurity

Challenge 9 - Scrambled Photo

Challenge 10 - Dance

Challenge 11 - Lasers

Challenge 12 - Victoria's Secret

Share on

Leave a Comment

You May Also Enjoy

Tuenti Challenge 8